Unidad 1.- Fundamentos de Circuitos Eléctricos
Circuitos Eléctricos
El circuito eléctrico es el recorrido preestablecido por por el que se desplazan las cargas eléctricas.
Circuito elemental
Las cargas eléctrica que constituyen una corriente eléctrica pasan de un punto que tiene mayor potencial eléctrico a otro que tiene un potencial inferior. Para mantener permanentemente esa diferencia de potencial, llamada también voltaje o tensión entre los extremos de un conductor, se necesita un dispositivo llamado generador (pilas, baterías, dinamos, alternadores...) que tome las cargas que llegan a un extremo y las impulse hasta el otro. El flujo de cargas eléctricas por un conductor constituye una corriente eléctrica.
Se distinguen dos tipos de corrientes:
Corriente continua: Es aquella corriente en donde los electrones circulan en la misma cantidad y sentido, es decir, que fluye en una misma dirección. Su polaridad es invariable y hace que fluya una corriente de amplitud relativamente constante a través de una carga. A este tipo de corriente se le conoce como corriente continua (cc) o corriente directa (cd), y es generada por una pila o batería.
Este tipo de corriente es muy utilizada en los aparatos electrónicos portátiles que requieren de un voltaje relativamente pequeño. Generalmente estos aparatos no pueden tener cambios de polaridad, ya que puede acarrear daños irreversibles en el equipo.
Corriente alterna: La corriente alterna es aquella que circula durante un tiempo en un sentido y después en sentido opuesto, volviéndose a repetir el mismo proceso en forma constante. Su polaridad se invierte periódicamente, haciendo que la corriente fluya alternativamente en una dirección y luego en la otra. Se conoce en castellano por la abreviación CA y en inglés por la de AC.
Este tipo de corriente es la que nos llega a nuestras casas y sin ella no podríamos utilizar nuestros artefactos eléctricos y no tendríamos iluminación en nuestros hogares. Este tipo de corriente puede ser generada por un alternador o dinamo, la cual convierten energía mecánica en eléctrica.
El mecanismo que lo constituye es un elemento giratorio llamado rotor, accionado por una turbina el cual al girar en el interior de un campo magnético (masa), induce en sus terminales de salida un determinado voltaje. A este tipo de corriente se le conoce como corriente alterna (a).
Circuitos RLC
En electrodinámica un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina (inductancia) y un condensador (capacitancia).
Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describen generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primer orden).
Con ayuda de un generador de señales, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento de la corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencial que lo rige).
Circuito sometido a un escalón de tensión
Si un circuito RLC en serie es sometido a un escalón de tensión {\displaystyle E\,} E\,, la ley de las mallas impone la relación:
CONDUCTOS ELÉCTRICOS Y SUS APLICACIONES
Un conductor eléctrico es un material que ofrece poca resistencia al movimiento de la carga eléctrica.

Son materiales cuya resistencia al paso de la electricidad es muy baja. Los mejores conductores eléctricos son metales, como el cobre, el oro, el hierro, la plata y el aluminio, y sus aleaciones, aunque existen otros materiales no metálicos que también poseen la propiedad de conducir la electricidad, como el grafito o las disoluciones y soluciones salinas (por ejemplo, el agua de mar) o cualquier material en estado de plasma.
Para el transporte de energía eléctrica, así como para cualquier instalación de uso doméstico o industrial, el mejor conductor es el cobre (en forma de cables de uno o varios hilos). Aunque la plata es el mejor conductor, pero debido a su precio elevado no se usa con tanta frecuencia. También se puede usar el aluminio, metal que si bien tiene una conductividad eléctrica del orden del 60% de la del cobre, es sin embargo un material tres veces más ligero, por lo que su empleo está más indicado en líneas aéreas que en la transmisión de energía eléctrica en las redes de alta tensión.1 A diferencia de lo que mucha gente cree, el oro es levemente peor conductor que el cobre; sin embargo, se utiliza en bornes de baterías y conectores eléctricos debido a su durabilidad y “resistencia” a la corrosión.
La conductividad eléctrica del cobre puro fue adoptada por la Comisión Electrotécnica Internacional en 1913 como la referencia estándar para esta magnitud, estableciendo el International Annealed Copper Standard (Estándar Internacional del Cobre Recocido) o IACS. Según esta definición, la conductividad del cobre recocido medida a 20 °C es igual a 58.0 MS/m.2 A este valor es a lo que se llama 100% IACS y la conductividad del resto de los materiales se expresa como un cierto porcentaje de IACS. La mayoría de los metales tienen valores de conductividad inferiores a 100% IACS pero existen excepciones como la plata o los cobres especiales de muy alta conductividad designados C-103 y C-110.3
UNIDAD 2.- ELECTRÓNICA ANALÓGICA
La electrónica analógica (a veces también electrónica análoga, por influencia del inglés) es una rama de la electrónica que estudia los sistemas cuyas variables (tensión, corriente, etcétera) varían de una forma continua en el tiempo y pueden tomar (al menos teóricamente) valores infinitos. En contraposición, en la electrónica digital las variables solo pueden tomar valores discretos y tienen siempre un estado perfectamente definido.
Por ejemplo: considerando una medida real concreta, como la longitud total de un coche:
En un sistema digital, esta medida podría ser de 4 metros o de 4 metros y 23 centímetros.
Es posible darle la exactitud deseada, pero siempre serán cantidades enteras.
En un sistema analógico, la medida en decimales seria 4,233648596... En teoría hasta que llegásemos a la mínima cantidad de materia existente (siempre que el sistema de medida sea lo suficientemente exacto).

Transistor bipolar, componente muy usado en los sistemas analógicos.
DIODOS SEMICONDUCTORES
Un diodo es un componente electrónico de dos terminales que permite la circulación de la corriente eléctrica a través de él en un solo sentido.1 Este término generalmente se usa para referirse al diodo semiconductor, el más común en la actualidad; consta de una pieza de cristal semiconductor conectada a dos terminales eléctricos. El diodo de vacío (que actualmente ya no se usa, excepto para tecnologías de alta potencia) es un tubo de vacío con dos electrodos: una lámina como ánodo, y un cátodo.
De forma simplificada, la curva característica de un diodo (I-V) consta de dos regiones: por debajo de cierta diferencia de potencial, se comporta como un circuito abierto (no conduce), y por encima de ella como un circuito cerrado con una resistencia eléctrica muy pequeña. Debido a este comportamiento, se les suele denominar rectificadores, ya que son dispositivos capaces de suprimir la parte negativa de cualquier señal, como paso inicial para convertir una corriente alterna en corriente continua. Su principio de funcionamiento está basado en los experimentos de Lee De Forest.
Los primeros diodos eran válvulas o tubos de vacío, también llamados válvulas termoiónicas constituidos por dos electrodos rodeados de vacío en un tubo de cristal, con un aspecto similar al de las lámparas incandescentes. El invento fue desarrollado en 1904 por John Ambrose Fleming, empleado de la empresa Marconi, basándose en observaciones realizadas por Thomas Alva Edison.
Al igual que las lámparas incandescentes, los tubos de vacío tienen un filamento (el cátodo) a través del cual circula la corriente, calentándolo por efecto Joule. El filamento está tratado con óxido de bario, de modo que al calentarse emite electrones al vacío circundante los cuales son conducidos electrostáticamente hacia una placa, curvada por un muelle doble, cargada positivamente (el ánodo), produciéndose así la conducción. Evidentemente, si el cátodo no se calienta, no podrá ceder electrones. Por esa razón, los circuitos que utilizaban válvulas de vacío requerían un tiempo para que las válvulas se calentaran antes de poder funcionar y las válvulas se quemaban con mucha facilidad.

Diodo en primer plano. Nótese la forma cuadrada del cristal semiconductor (objeto negro de la izquierda)
AMPLIFICADORES OPERACIONALES
Un amplificador operacional, a menudo conocido op-amp por sus siglas en inglés (operational amplifier) es un dispositivo amplificador electrónico de alta ganancia acoplado en corriente continua que tiene dos entradas y una salida. En esta configuración, la salida del dispositivo es, generalmente, de cientos de miles de veces mayor que la diferencia de potencial entre sus entradas.

Amplificador operacional modelo LM741CN de National Semiconductor con encapsulado plástico DIP

Terminales
V+: Entrada no inversora
V−: Entrada inversora
Vout: Salida
VS+: Fuente DC positiva
VS−: Fuente DC negativa
Los diseños varían entre cada fabricante y cada producto, pero todos los amplificadores operacionales tienen básicamente la misma estruct ura interna, que consiste en tres etapas
ura interna, que consiste en tres etapas
 ura interna, que consiste en tres etapas
ura interna, que consiste en tres etapas
:
Amplificador diferencial: es la etapa de entrada que proporciona una baja amplificación del ruido y gran imped ancia de entrada. Suelen tener una salida diferencial.
ancia de entrada. Suelen tener una salida diferencial.
 ancia de entrada. Suelen tener una salida diferencial.
ancia de entrada. Suelen tener una salida diferencial.
Amplificador de tensión: proporciona ganancia de tensión.
Amplificador de salida: proporciona la capacidad de suministrar la corriente necesaria, tiene una baja impedancia de salida y, usualmente, protección frente a cortocircuitos. Éste también proporciona una ganancia adicional.
ELECTRÓNICA DIGITAL
La electrónica digital es la rama de la electrónica más moderna y que evoluciona más rápidamente. Se encarga de sistemas electrónicos en los que la información está codificada en estados discretos, a diferencia de los sistemas analógicos donde la información toma un rango continuo de valores.
En la mayoría de sistemas digitales, el número de estados discretos es tan solo de dos y se les denomina niveles lógicos. Estos niveles se representan por un par de valores de voltaje, uno cercano al valor de referencia del circuito (normalmente 0 voltios, tierra o "GND"), y otro cercano al valor dado por la fuente de alimentación del circuito. Estos dos estados discretos reciben muchas parejas de nombres en libros de electrónica y otros textos especializados, siendo los más comunes "0" y "1", "false" y "true", "off" y "on" o "bajo" y "alto" entre otros. Tener solo estos dos valores nos permiten usar el Álgebra Booleana y códigos binarios, los que nos proporciona herramientas muy potentes para realizar cálculo sobre las señales de entrada.
Al hablar de electrónica digital estamos en presencia del mayor avance en cuanto a ciencia electrónica se refiere. Al principio los mecanismos interactuaban entre si por movimientos y secuencia preconcebidas para obtener un mismo resultado, la invención de las válvulas, luego los transistores, los chips y por último los microprocesadores así como los micro-controladores han llevado a esta ciencia a posicionarse como una de las más precisas en lo que a procesamiento de datos, imagen y vídeo podamos hablar.
Los más complejos sistemas digitales, aplicados y útiles hoy en día son posibles gracias a la integración de los componentes, herramientas, equipos y subsistemas electrónicos, informáticos y mecánicos. En tiempos modernos es tan fácil tocar una pantalla con nuestras manos (pantalla táctil), ejecutar un comando de voz y cambiar un canal o abrir una ventana, apagar y encender una bombilla; todo gracias a la electrónica digital. Como su nombre lo indica ella se sustenta en su propio lenguaje, el lenguaje de código binario "1" y "0", se crean ciclos de palabras, password, secuencias de bit y byte y se hace realidad lo que nunca se pensó poder monitorear en tiempo real un proceso a miles de kilómetros de distancia. Todas las demás ciencias hoy en día se deben a la invención de los sistemas digitales, es difícil pensar en cocinar algo, llamar a un pariente lejano o ir al cine sin dejar a un lado la electrónica digital.
Por eso podemos decir que ella misma contempla los mejores avances y conducen la vida al futuro, claro complementada por las telecomunicaciones y por las ciencias exactas, la informática, la mecatrónica, la ciencia médica con aplicaciones de prótesis, chips cerebrales, los mismos juegos de realidad virtual y videojuegos infantiles y los no tan infantiles. En conclusión los desarrollos tecnológicos gestados en laboratorios, instalaciones militares, los avances y ayudas humanitarias a países y personas en sitios aun hoy en día remotos e inhóspitos, no fueran posible sin esta rama de la ingeniería la electrónica pero principalmente la digital, la cual es hoy en día una de las más importantes, versátil y sigue en avance y crecimiento en tiempos globalizados.
La electrónica digital ha alcanzado una gran importancia debido a que es utilizada para realizar autómatas y por ser la piedra angular de los sistemas microprogramados como son los ordenadores o computadoras.
Los sistemas digitales pueden clasificarse del siguiente modo:
Sistemas cableados
Combinacionales
Secuenciales
Memorias
Convertidores
Sistemas programados
Microprocesadores
Microcontroladores

Circuito digital de un reloj binario en una placa de pruebas.

Controlador digital industrial
TABLAS DE VERDAD
Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.1
Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.
Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:
Como razonamientos deductivos lógico-lingüísticos
Como construcción de un sistema matemático puro
Como una aplicación lógica en un Circuito de conmutación.
Verdadero[editar]
TE Conex 12.svg TE Interu 05.svg TE Conex 12.svg
El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.



Falso
El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.



Variable
 |  |  |
Para una variable lógica A, B, C, ... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:
Negación
 |  |  |
La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.
Conjunción
 |  |  |  |
La conjunción es un operador, que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir, es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:
Que se corresponde con la columna 8 del algoritmo fundamental.
en simbología "^" hace referencia a el conector "y"
Disyunción
 |  |  |  |
 |  |  |  |
La disyunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:
Que se corresponde con la columna 2 del algoritmo fundamental.
Implicación o Condicional
 |  |  |  |
 |  |  |  |
El condicional material es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:
Que se corresponde con la columna 5 del algoritmo fundamental.
Equivalencia, doble implicación o Bicondicional
 |  |  |  |
 |  |  |  |
El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad son diferentes.
La tabla de verdad del bicondicional es la siguiente:
Que se corresponde con la columna 7 del algoritmo fundamental.
PUERTAS LÓGICAS
Una puerta lógica, o compuerta lógica, es un dispositivo electrónico con una función booleana. Suman, multiplican, niegan o afirman, incluyen o excluyen según sus propiedades lógicas. Se pueden aplicar a tecnología electrónica, eléctrica, mecánica, hidráulica y neumática. Son circuitos de conmutación integrados en un chip. Experimentaba con relés o interruptores electromagnéticos para conseguir las condiciones de cada compuerta lógica, por ejemplo, para la función booleana Y (AND) colocaba interruptores en circuito serie, ya que con uno solo de éstos que tuviera la condición «abierto», la salida de la compuerta Y sería = 0, mientras que para la implementación de una compuerta O (OR), la conexión de los interruptores tiene una configuración en circuito paralelo.
La tecnología microelectrónica actual permite la elevada integración de transistores actuando como conmutadores en redes lógicas dentro de un pequeño circuito integrado. El chip de la CPU es una de las máximas expresiones de este avance tecnológico.
En nanotecnología se está desarrollando el uso de una compuerta lógica molecular, que haga posible la miniaturización de circuitos.
Puerta SÍ o BUFFER
La puerta lógica SÍ, realiza la función booleana igualdad. En la práctica se suele utilizar como amplificador de corriente o como seguidor de tensión, para adaptar impedancias (buffer en inglés).
La ecuación característica que describe el comportamiento de la puerta SÍ es:
Su tabla de verdad es la siguiente:
| Entrada | Salida |
|---|---|
Puerta AND
La puerta lógica Y, más conocida por su nombre en inglés AND (), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
La ecuación característica que describe el comportamiento de la puerta AND es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Así, desde el punto de vista de la aritmética módulo 2, la compuerta AND implementa el producto módulo 2.
Puerta OR
La puerta lógica O, más conocida por su nombre en inglés OR (), realiza la operación de suma lógica.
La ecuación característica que describe el comportamiento de la puerta OR es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Podemos definir la puerta O como aquella que proporciona a su salida un 1 lógico si al menos una de sus entradas está a 1.
Puerta OR-exclusiva (XOR)
La puerta lógica OR-exclusiva, más conocida por su nombre en inglés XOR, realiza la función booleana A'B+AB'. Su símbolo es (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta XOR es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Se puede definir esta puerta como aquella que da por resultado uno, cuando los valores en las entradas son distintos. ej: 1 y 0, 0 y 1 (en una compuerta de dos entradas). Se obtiene cuando ambas entradas tienen distinto valor.
Si la puerta tuviese tres o más entradas, la XOR tomaría la función de suma de paridad, cuenta el número de unos a la entrada y si son un número impar, pone un 1 a la salida, para que el número de unos pase a ser par. Esto es así porque la operación XOR es asociativa, para tres entradas escribiríamos: a(bc) o bien (ab)c. Su tabla de verdad sería:
| Entrada | Entrada | Entrada | Salida |
|---|---|---|---|
Desde el punto de vista de la aritmética módulo 2, la puerta XOR implementa la suma módulo 2, pero mucho más simple de ver, la salida tendrá un 1 siempre que el número de entradas a 1 sea impar.
Puerta NOR-exclusiva (XNOR)
La puerta NOR exclusive, Conocida por su referencia en inglés XNOR, es el complemento de la puerta OR exclusiva, siendo su función booleana AB + A’B’. Se utiliza el mismo símbolo que la puerta OR exclusiva (signo más “+” inscrito en un círculo) y su representación en el diseño de circuitos lógicos y ecuación que la describe.
o también como:
Las tablas de verdad para dos y tres entradas o variables son las siguientes:
| Entrada | Entrada | |
|---|---|---|
0
|
0
|
1
|
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| Entrada | Entrada | Entrada | Salida |
|---|---|---|---|
| 0 | 0 |
0
| 1 |
0
|
0
|
1
| 0 |
0
|
1
|
0
| 0 |
0
|
1
|
1
| 1 |
1
| 0 |
0
| 0 |
1
|
0
|
1
| 1 |
1
|
1
|
0
| 1 |
1
|
1
|
1
| 0 |
Esta puerta al ser el complemento de la puerta OR exclusiva (XOR), sus resultados son uno (1) cuando sus entradas, para el caso de 2, son iguales, ya sean con valor 0 o valor 1 (0 y 0, ó 1 y 1). Para más de 2 entradas, si el número de unos de entradas es par, la salida es 1 y si es impar, la salida es 0. Si todas las entradas son 0, la salida es 1, como puede comprobarse en la tabla de verdad de tres entradas.
La puerta lógica XNOR se identifica como función par, en tanto que la puerta lógica XOR se identifica como función impar.
Lógica negada
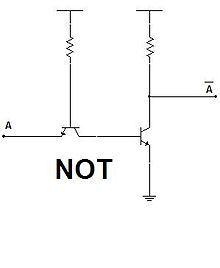
Puerta NO (NOT)
La puerta lógica NO (NOT en inglés) realiza la función booleana de inversión o negación de una variable lógica. Una variable lógica (A)a la cual se le aplica la negación se pronuncia como "no A" o "A negada".
La ecuación característica que describe el comportamiento de la puerta NOT es:
Su tabla de verdad es la siguiente:
| Entrada | Salida |
|---|---|
Se puede definir como una puerta que proporciona el estado inverso del que esté en su entrada.
Puerta NO-Y (NAND)
La puerta lógica NO-Y, más conocida por su nombre en inglés NAND, realiza la operación de producto lógiconegado. En ocasiones es llamada también barra de Sheffer.1 En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta NAND es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Podemos definir la puerta NO-Y como aquella que proporciona a su salida un 0 lógico únicamente cuando todas sus entradas están a 1.
Puerta NO-O (NOR)
La puerta lógica NO-O, más conocida por su nombre en inglés NOR, realiza la operación de suma lógica negada. En ocasiones es llamada también barra de Pierce.2 En la figura de la derecha pueden observarse sus símbolos en electrónica.
La ecuación característica que describe el comportamiento de la puerta NOR es:
Su tabla de verdad es la siguiente:
| Entrada | Entrada | Salida |
|---|---|---|
Podemos definir la puerta NO-O como aquella que proporciona a su salida un 1 lógico sólo cuando todas sus entradas están a 0. La puerta lógica NOR constituye un conjunto completo de operadores.
Conjunto de puertas lógicas completo
Un conjunto de puertas lógicas completo es aquel con el que se puede implementar cualquier función lógica. A continuación se muestran distintos conjuntos completos (uno por línea):
- Puertas AND, OR y NOT.
- Puertas AND y NOT.
- Puertas OR y NOT.
- Puertas NAND.
- Puertas NOR.
Además, un conjunto de puertas lógicas es completo si puede implementar todas las puertas de otro conjunto completo conocido. A continuación se muestran las equivalencias al conjunto de puertas lógicas completas con las funciones NAND y NOR.
| Salida función | Salida función | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | ||
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Mapa de Karnaugh
Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.
Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.
El mapa de Karnaugh consiste en una representación bidimensional de la tabla de verdad de la función a simplificar. Puesto que la tabla de verdad de una función de N variables posee 2N filas, el mapa K correspondiente debe poseer también 2N cuadrados. Las variables de la expresión son ordenadas en función de su peso y siguiendo el código Gray, de manera que sólo una de las variables varía entre celdas adyacentes. La transferencia de los términos de la tabla de verdad al mapa de Karnaugh se realiza de forma directa, albergando un 0 ó un 1, dependiendo del valor que toma la función en cada fila. Las tablas de Karnaugh se pueden fácilmente realizar a mano con funciones de hasta 6 variables, para funciones de mayor cantidad de variables es más eficiente el uso de software especializado.
 Ejemplo de mapa de Karnaugh.
Ejemplo de mapa de Karnaugh.
Minitérminos
Para una función booleana de n variables x1,...xn, un producto booleano en el que cada una de las n variables aparece una sola vez (negada o sin negar) es llamado minterms. Es decir, un minterms es una expresión lógica de n variables consistente únicamente en el operador conjunción lógica (AND) y el operador complemento o negación (NOT).
Por ejemplo, abc, ab'c y abc' son ejemplos de minterms para una función booleana con las tres variables a, b y c.
En general, uno asigna a cada minterm (escribiendo las variables que lo componen en el mismo orden), un índice basado en el valor binario del minterm. un término negado, como a' es considerado como el numero binario 0 y el término no negado a es considerado como un 1. Por ejemplo, se asociaría el número 6 con a b c'(1102), y nombraríamos la expresión con el nombre m6. Entonces m0 de tres variables es a'b'c'(0002) y m7 debería ser a b c(1112).
Función equivalente
Se puede observar que cada minterm solo devuelve 'verdadero' con una sola entrada de las posibles. Por ejemplo, el minterm 5, a b' c, es verdadero solo cuando a y c son ciertos y b es falso - la entrada a = 1, b = 0, c = 1 da resultado 1.gff
Si tenemos una tabla de verdad de una función lógica, es posible escribir la función como "suma de productos". Por ejemplo, dada la tabla de verdad
a b f(a, b)
0 0 1
0 1 0
1 0 1
1 1 0
Observamos que las filas con resultado 1 son la primera y la tercera, entonces podremos escribir f como la suma de los minterms m0 y m2.
Si queremos verificar esto:
f(a,b) = m0 + m2 = (a'b')+(ab')
Tendremos que la tabla de verdad de la función, calculándola directamente, será la misma.
MAXITERMINOS
Un maxterm es una expresión lógica de n variables que consiste únicamente en la disyunción lógica y el operador complemento o negación. Los maxterms són una expresión dual de los minterms. En vez de usar operaciones AND utilizamos operaciones OR y procedemos de forma similar.
Por ejemplo, los siguientes son maxterms:
a+b'+c
a'+b+c
El complemento de un minterm es su respectivo maxterm. Esto puede ser fácilmente verificado usando la Ley de Morgan. Por ejemplo:
m1' = M1
(a'b)' = a+b'
Para indexar maxterms lo haremos justo de la forma contraria a la que seguimos con los minterms. Se asigna a cada maxterm un índice basado en el complemento del número binario que representa (otra vez asegurándonos que las variables se escriben en el mismo orden, usualmente alfabético). Por ejemplo, podemos asignar M6 (Maxterm 6) al maxterm a'+b'+c. De forma similar M0 de tres variables debería ser a+b+c y M7 es a'+b'+c'.
1. Sección osciladora.
2. Sección amplificadora.
3. Sección elevadora de voltaje.
4. Sección proveedora de corriente directa.
5. Sección proveedora de corriente alterna.
Sección osciladora:
Esta se encarga de generar los pulsos o ciclos necesarios para que la corriente alterna que provea el inversor sea igual a la corriente alterna que provee la empresa del servicio eléctrico, para unos paises es de 50 ciclos y en otros 60 ciclos.
Sección amplificadora:
La función de esta sección es la de amplificar los pulsos para excitar a la sección elevadora de voltaje.
Sección elevadora de voltaje:
Esta se encarga de elevar el voltaje a 120 o 220, según sea el caso, función que está a cargo de un transformador, que cuando hay energía externa, se encarga de cargar la batería, apoyado por un circuito electrónico que al estar completamente cargada la batería, se desconecta automáticamente. Al faltar el suministro de energía público, el cargador invierte su función y se encarga de elevar el voltaje.
Sección proveedora de corriente directa:.
Esta no es otra cosa que la batería propiamente dicha.
Sección proveedora de corriente alterna:
Es la que recibimos de la empresa encargada de prestar el servicio eléctrico.
En estas páginas se publicarán circuitos electrónicos de este tipo y esperamos que sean de utlidad para todos.
CONVERTIDORES
Un inversor o convertidor es un equipo electrónico que convierte la corriente directa de una batería ( acumulador ), en corriente alterna tal como la recibimos de la empresa proveedora de energía eléctrica. La UPS ( Uninterrumpible Power Supply ), que se utiliza para suministrarle energía a una computadora en momentos de falta del suministro público, no es otra cosa que un inversor convertidor, estos equipos se componen de varias secciones:1. Sección osciladora.
2. Sección amplificadora.
3. Sección elevadora de voltaje.
4. Sección proveedora de corriente directa.
5. Sección proveedora de corriente alterna.
Sección osciladora:
Esta se encarga de generar los pulsos o ciclos necesarios para que la corriente alterna que provea el inversor sea igual a la corriente alterna que provee la empresa del servicio eléctrico, para unos paises es de 50 ciclos y en otros 60 ciclos.
Sección amplificadora:
La función de esta sección es la de amplificar los pulsos para excitar a la sección elevadora de voltaje.
Sección elevadora de voltaje:
Esta se encarga de elevar el voltaje a 120 o 220, según sea el caso, función que está a cargo de un transformador, que cuando hay energía externa, se encarga de cargar la batería, apoyado por un circuito electrónico que al estar completamente cargada la batería, se desconecta automáticamente. Al faltar el suministro de energía público, el cargador invierte su función y se encarga de elevar el voltaje.
Sección proveedora de corriente directa:.
Esta no es otra cosa que la batería propiamente dicha.
Sección proveedora de corriente alterna:
Es la que recibimos de la empresa encargada de prestar el servicio eléctrico.
En estas páginas se publicarán circuitos electrónicos de este tipo y esperamos que sean de utlidad para todos.













 ), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.
), realiza la función booleana de producto lógico. Su símbolo es un punto (·), aunque se suele omitir. Así, el producto lógico de las variables A y B se indica como AB, y se lee A y B o simplemente A por B.



 ), realiza la operación de suma lógica.
), realiza la operación de suma lógica.

 (signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en
(signo más "+" inscrito en un círculo). En la figura de la derecha pueden observarse sus símbolos en 





 o también como:
o también como: 













No hay comentarios:
Publicar un comentario